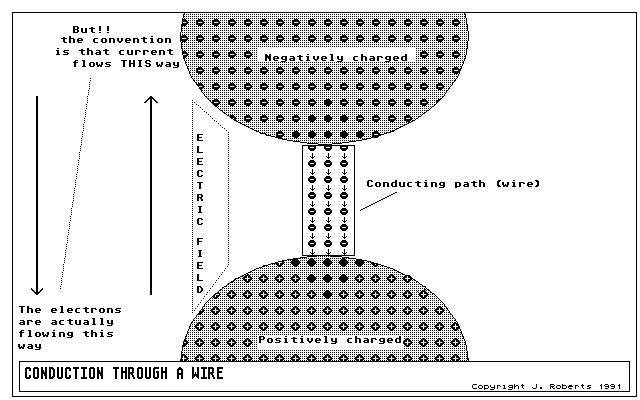
Figure 1: here we see the charged spheres from before, with a conducting pathway joining them. What happens? A electric current flows.

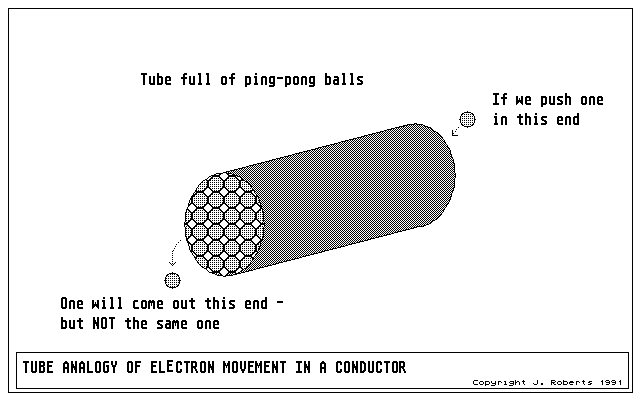Figure 2: an analogy for how electrons can move slowly, yet the ripple of movement travel very much faster. Push a ball in one end of a full tube - and out pops another at the other end. Remember that this is an analogy; electrons aren't ping-pong balls, and more problematically, there's no way to tell one from another...

Figure 3: resistance is simply proportional (all else being equal) to the quantity of conductor available. Increase the quantity of conductor and reduce the resistance, and vice versa.

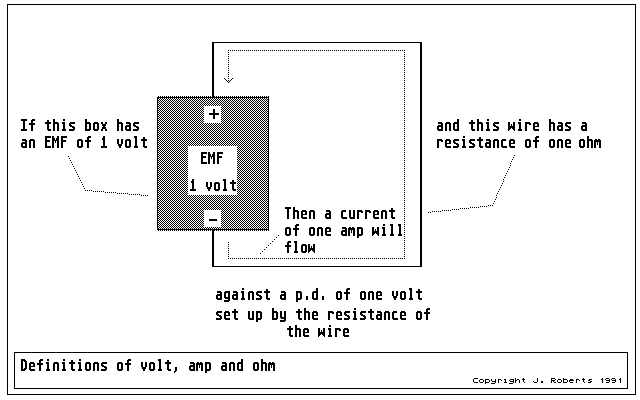Figure 4: the legacy of Mr. Volta, Ampere and Ohm: the volt, amp and ohm.

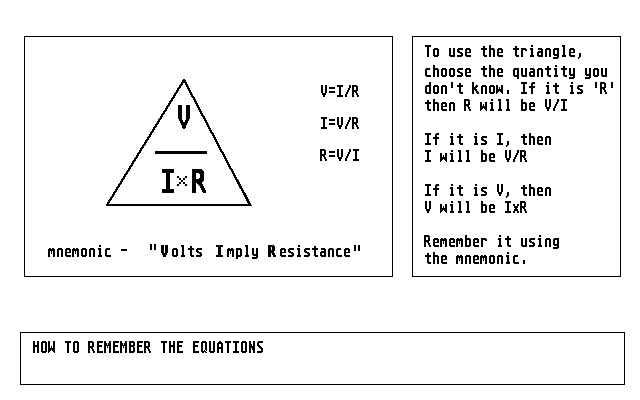Figure 5: a way to remember the equation usually known as "Ohms Law": volts imply resistance.

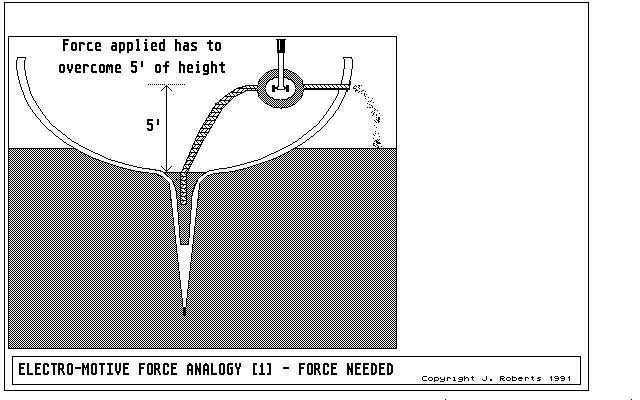Figure 6: electro-motive force compared with water-motive force

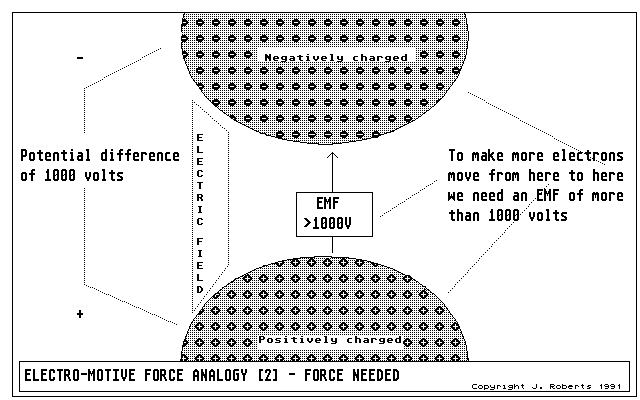Figure 7: the charged conducting spheres; to make electrons travel against a particular pd, we need a larger emf.

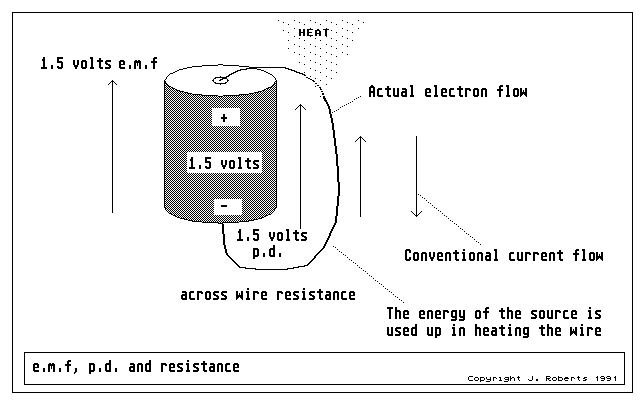Figure 8: an emf with a completed circuit causes a current which generates a pd across the connection

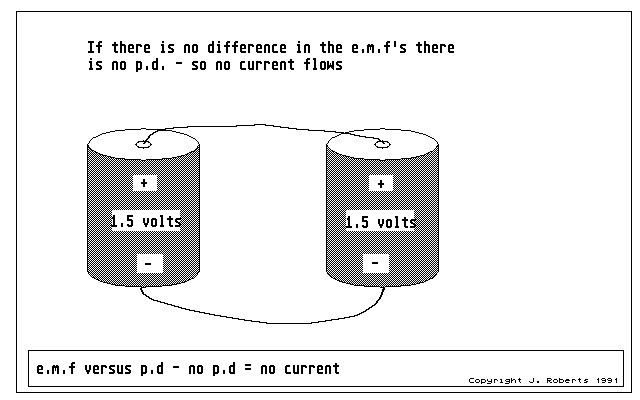Figure 9: emf and pd are rather closely related - no difference in emf means no pd

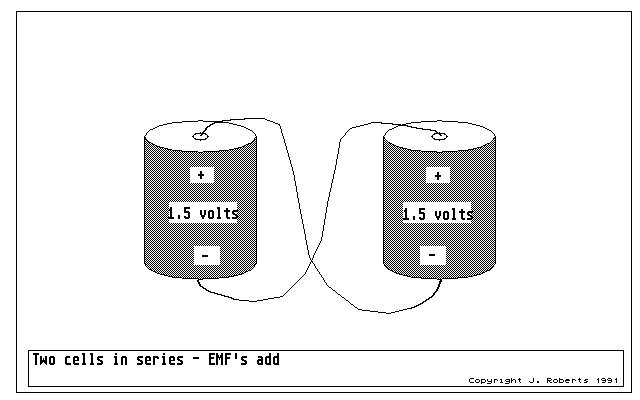Figure 10: emf's can simply add and subtract

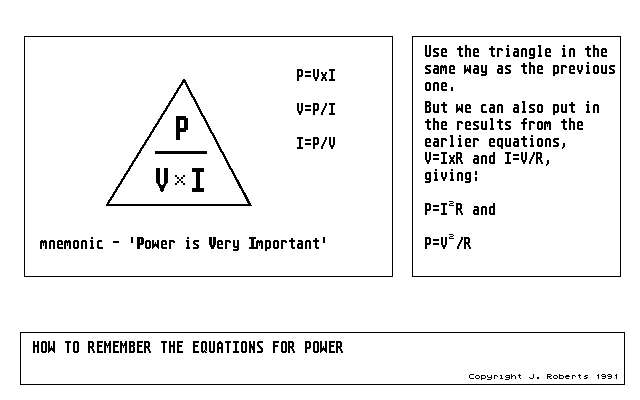Figure 11: the power equation starts out just like Ohm's Law: power is very important

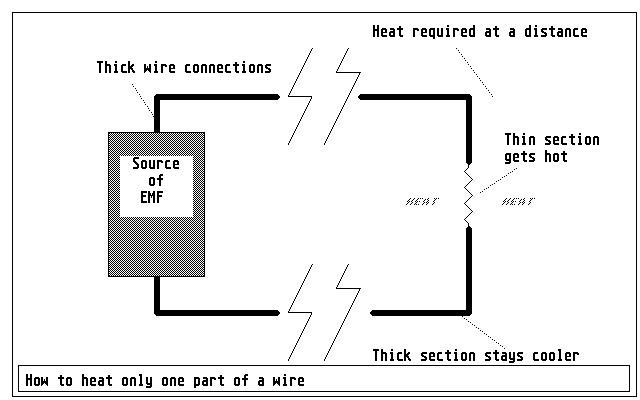Figure 12: by manipulating the characteristics of pieces of wire, we can ensure that the heating effect mostly happens in the place where it's useful to us

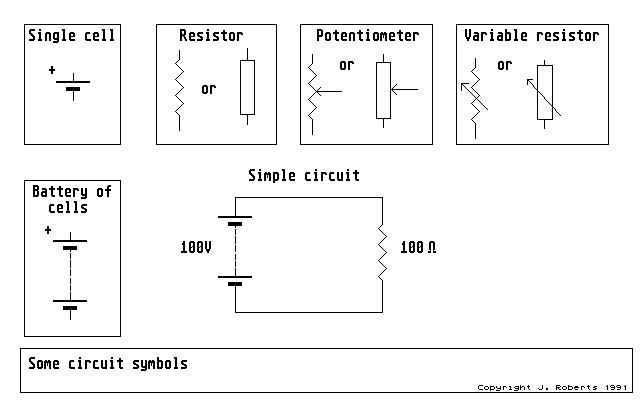Figure 13: representative circuit symbols

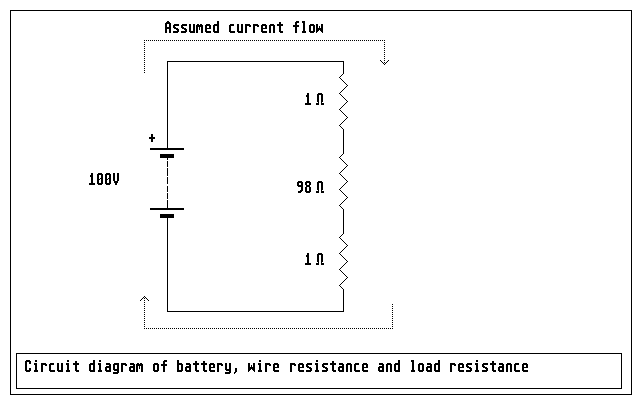Figure 14: a idealised circuit with a battery providing emf with three resitances connected to it

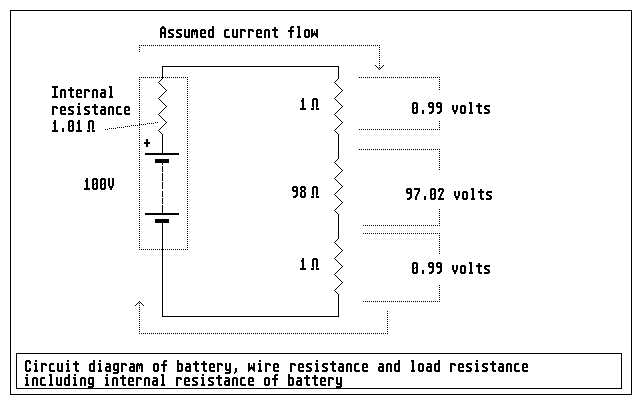Figure 15: a less idealised battery, with its internal resistance included, changes the results

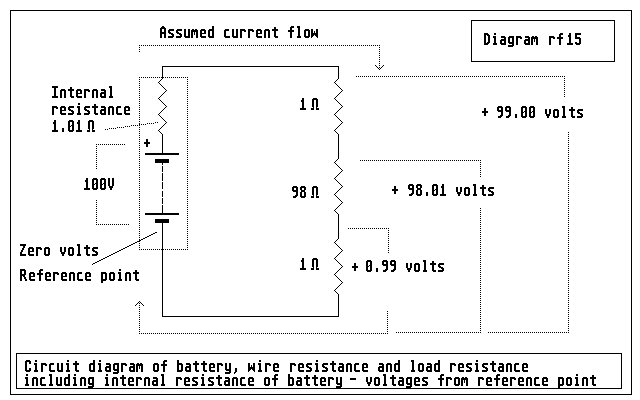Figure 16: voltages can be added and subtracted as long as they are related (or "referred") to the same reference point

Figure 17: [a] dividing potential by means of two resistances [b] a "potentiometer" is a resistance with a moving contact - best known as the humble volume control

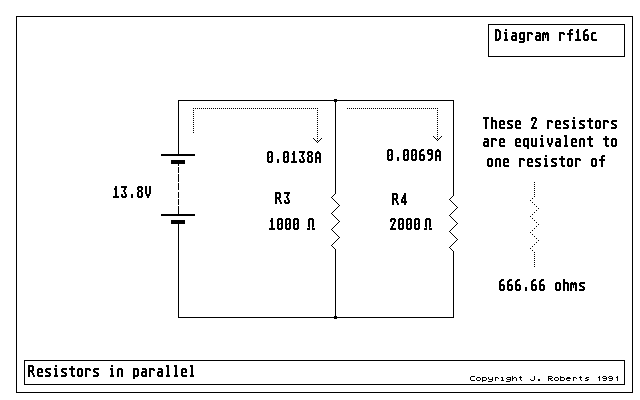Figure 18: two resistances in parallel are equivalent to a smaller resistance

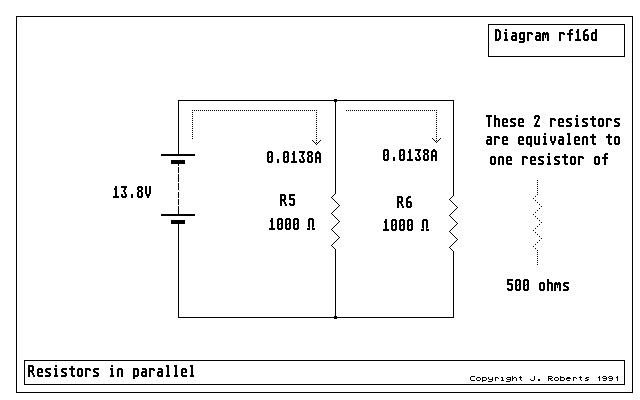Figure 19: two identical resistances in parallel are equivalent to one of exactly half the value

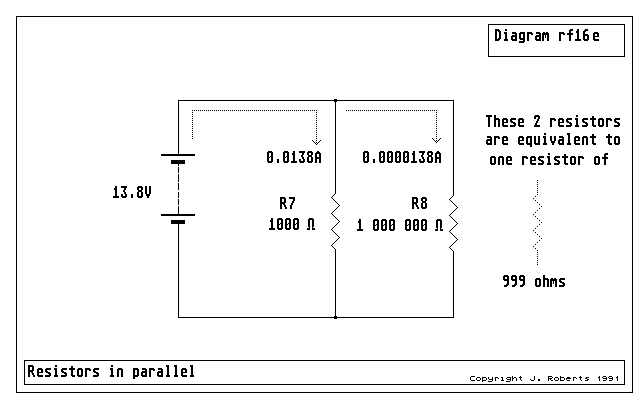Figure 20: a very large resistance in parallel with a small one barely affects the overall value

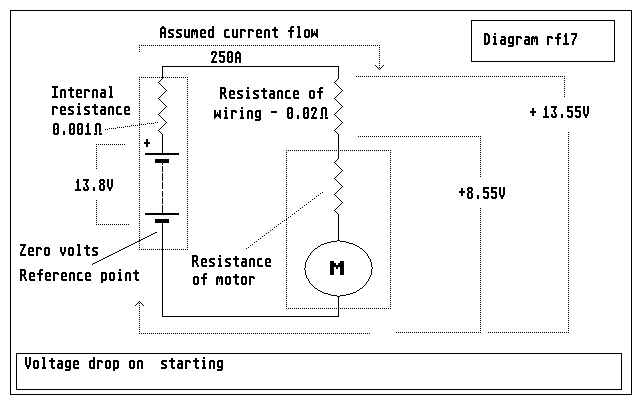Figure 21: getting real: a fairly realistic set of values for the starting motor circuit of an engine